A função do 2º grau, também denominada função quadrática, é definida pela expressão do tipo:
y = f(x) = ax² + bx + c, onde a, b e c são constantes reais e  |
a) y=x²+3x+2 ( a=1; b=3; c=2 )
b) y=x² ( a=1; b=0; c=0 )
c) y=x²-4 ( a=1; b=0; c=-4 )
Gráfico de uma função do 2º grau:
O gráfico de uma função quadrática
é uma parábola |
Podemos visualizar uma parábola em um parque de diversões, simplesmente olhando para a montanha russa.
Sua representação gráfica é dada em torno de eixos:
Exemplo:
Construa o gráfico da função y=x²:
[Sol] Como na função do 1º grau, basta atribuir valores reais para x, obtemos seus valores correspondentes para y.
x | y = f(x) = x² |
-2 | 4 |
-1 | 1 |
0 | 0 |
1 | 1 |
2 | 4 |
3 | 9 |
| |
Coordenadas do vértice
A coordenada x do vértice da parábola pode ser determinada por  . .
Exemplo: Determine as coordenada do vértice da parábola y=x²-4x+3
Temos: a=1, b=-4 e c=3
Logo, a coordenada x será igual a 2, mas e a coordenada y? Simples: Vamos substituir o valor obtido da coordenada x e determinar o valor da coordenada y. Assim, para determinarmos a coordenada y da parábola
y=x²-4x+3, devemos substituir o valor de x por 2. y = (2)²-4.(2)+3 = 4-8+3=-1 Logo, as coordenadas do vértice serão V=(2,-1) Portanto, para determinarmos as coordenadas do vértice de uma parábola, achamos o valor da coordenada x (através de x=-b/2a) e substituindo este valor na função, achamos a coordenada y!!! Raízes (ou zeros) da função do 2º grau Denominam-se raízes da função do 2º grau os valores de x para os quais ela se anula. y=f(x)=0 Exemplo: na função y=x²-4x+3, que acima acabamos de determinar as coordenadas de seus vértices, as raízes da função serão x=1 e x`=3. Vejamos o gráfico: Notem que quando x=1 e x`=3, a parábola intercepta ("corta") o eixo x. Como determinar a raiz ou zero da função do 2º grau? Simplesmente aplicando a resolução de equações do 2º grau, já vista na seção anterior. Exemplo: determine a raiz da função y=x²+5x+6: Fazendo y=f(x)=0, temos x²+5x+6=0 Agora basta resolver a equação aplicando a fórmula de Bháskara. x²+5x+6=0 Acharemos que x = -2 e x` = -3.
Concavidade da parábola
Explicarei esta parte com um simples desenho.

| 
|
| a>0 | a<0 |
Os desenhos até que ficaram bonitinhos, mas isso não importa neste momento. O que nos importa agora é que quando a>0, a concavidade da parábola está voltada para cima (carinha feliz) e quando a<0, a parábola está voltada para baixo (carinha triste).
Exemplos:
| y = f(x) = x² - 4 |
| |
| a = 1 >0 |
| y = f(x) = -x² + 4 |
| |
| a = -1 < 0 |
[Nota] Quando a concavidade está voltada para cima (a>0), o vértice representa o valor mínimo da função. Quando a concavidade está voltada para baixo (a<0), o vértice representa o valor máximo.
Quando o discriminante é igual a zero
Quando o valor de  , o vértice a parábola encontra-se no eixo x. A coordenada y será igual a zero. , o vértice a parábola encontra-se no eixo x. A coordenada y será igual a zero.
Exemplo: y=f(x)=x²+2x+1
x²+2x+1=0

x=x`=-b/2a=-1 As coordenadas do vértice serão V=(-1,0) Gráfico: Quando o discrimintante é maior que zero Quando o valor de  , a parábola intercepta o eixo x em dois pontos. (São as raízes ou zeros da função vistos anteriormente). , a parábola intercepta o eixo x em dois pontos. (São as raízes ou zeros da função vistos anteriormente). Exemplo: y = f(x) = x²-4x+3 x²-4x+3=0

x=1, x`=3 Gráfico: Quando o discriminante é menor que zero Quando o valor de  , a parábola não intercepta o eixo x. Não há raízes ou zeros da função. , a parábola não intercepta o eixo x. Não há raízes ou zeros da função. Exemplo: y = f(x) = x²-x+2 x²-x+2=0
 Gráfico: Resumindo:
Esboçando o gráfico
Para finalizarmos (ufa!), vamos desenhar o gráfico da função
y=-x²-4x-3
1ª etapa: Raízes ou zeros da função
-x²-4x-3=0
Aplicando a fórmula de Bháskara
x=-1, x`=-3 2ª etapa: Coordenadas do vértice Coordenada x (=-b/2a): -(-4)/2.(-1)=-2 Coordenada y: Basta substituir o valor de x obtido na função
y = -x²-4x-3 = -(-2)²-4.(-2)-3 = -4+8-3 = 1 Portanto, V=(-2,1) 3ª etapa: Concavidade da parábola y=-x²-4x-3
Como a=-1<0, a concavidade estará voltada para baixo Feito isso, vamos esboçar o gráfico: | 















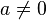






 .
.






 , o vértice a parábola encontra-se no eixo x. A coordenada y será igual a zero.
, o vértice a parábola encontra-se no eixo x. A coordenada y será igual a zero.

 , a parábola intercepta o eixo x em dois pontos. (São as raízes ou zeros da função vistos anteriormente).
, a parábola intercepta o eixo x em dois pontos. (São as raízes ou zeros da função vistos anteriormente).
 , a parábola não intercepta o eixo x. Não há raízes ou zeros da função.
, a parábola não intercepta o eixo x. Não há raízes ou zeros da função.













