escola: omega Alunos: Marcelline fanny e Rodrigo M. professor: luciano Reis disciplina: matemática série:9º
sábado, 24 de julho de 2010
SEGMENTOS PROPORCIONAIS
Proporção é a igualdade entre duas razões equivalentes. De forma semelhante aos que já estudamos com números racionais, é possível eatabelecer a proporcionalidade entre segmentos de reta, através das medidas desse segmentos. Vamos considerar primeiramente um caso particular com quatro segmentos de reta:
A razão entre os segmentos AB e CD e a razão entre os segmentos PQ e RS, são dadas por frações equivalentes, isto é:
AB/CD = 2/3
PQ/RS = 4/6 e como 2/3 = 4/6, segue a existência de uma proporção entre esses quatro segmentos de reta. Isto nos conduz à definição de segmentos proporcionais.
Diremos que quatro segmentos de reta, AB, BC, CD e DE, nesta ordem, são proporcionais se:
AB/BC = CD/DE Os segmentos AB e DE são os segmentos extremos e os segmentos BC e CD são os segmentos meios.
A proporcionalidade acima é garantida pelo fato que existe uma proporção entre os números reais que representam as medidas dos segmentos:
Propriedade Fundamental das proporções: Numa proporção de segmentos, o produto das medidas dos segmentos meios é igual ao produto das medidas dos segmentos extremos.
m(AB) . m(DE) = m(BC) . m(CD)
| m(AB)=2 cm | A ______ B | P __________ Q | m(PQ)=4 cm |
|---|---|---|---|
| m(CD)=3 cm | C __________ D | R ___________________ S | m(RS)=6 cm |
PQ/RS = 4/6
Diremos que quatro segmentos de reta, AB, BC, CD e DE, nesta ordem, são proporcionais se:
A proporcionalidade acima é garantida pelo fato que existe uma proporção entre os números reais que representam as medidas dos segmentos:
| m(AB) | m(CD) | |
|---|---|---|
| = | ||
| m(BC) | m(DE) |
RETAS PARALELAS CORTADAS POR UMA TRANVERSAL
TEOREMA DE TALES
O Teorema de Tales possui diversas aplicações no cotidiano, constituindo uma importante ferramenta da Geometria no cálculo de distâncias inacessíveis e nas relações envolvendo semelhança entre triângulos.
Exemplos:
Calcule o comprimento da ponte que deverá ser construída sobre o rio, de acordo com o esquema a seguir.
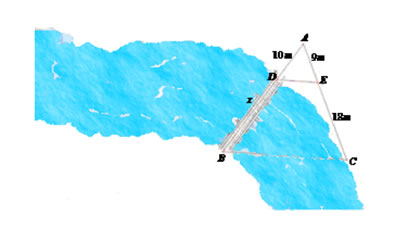
De acordo com a figura temos um triângulo ABC e o segmento DE dividindo o triângulo, sendo formado o triângulo ADE. As informações que temos são as medidas dos seguintes segmentos: AD = 10m, AE = 9m, EC = 18m e DB = x. O valor de DB será determinado através do Teorema de Tales que diz: “retas paralelas cortadas por transversais formam segmentos proporcionais.” Desse modo, podemos estabelecer a seguinte relação:
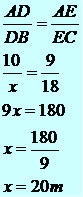
Portanto, a ponte terá 20 metros de comprimento.
Exemplos:
Calcule o comprimento da ponte que deverá ser construída sobre o rio, de acordo com o esquema a seguir.

De acordo com a figura temos um triângulo ABC e o segmento DE dividindo o triângulo, sendo formado o triângulo ADE. As informações que temos são as medidas dos seguintes segmentos: AD = 10m, AE = 9m, EC = 18m e DB = x. O valor de DB será determinado através do Teorema de Tales que diz: “retas paralelas cortadas por transversais formam segmentos proporcionais.” Desse modo, podemos estabelecer a seguinte relação:
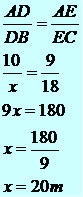
Portanto, a ponte terá 20 metros de comprimento.
EQUAÇÕES IRRACIONAIS
Vamos falar um pouco sobre Equações irracionais:
Antes de resolver uma equação assim temos que saber alguns assuntos que podemos chamar de pré-requisitos, e são eles: As quatro operações, potência, simplificação com radicais, operações com radicais, equações do primeiro e segundo graus e soma e produto dessas raízes, noções de função e zero da função. Depois de estudar esses assuntos fica muito fácil resolver uma equação irracional.
Equação irracional é aquela que no radical, nós encontramos uma incógnita, ou seja, uma letra.
Ex: √x = 15
Agora vamos ver como resolver uma equação irracional:
√x+3 = x-3
(√x+3)² =(x+3)² -->Iguala a potencia de acordo com o indice da raiz.
x+3 = x²-6x+9 -->Iguala a raiz a zero,reduzindo os termos.
x²-7x+6 = 0 -->Resolve fazendo a formula de Baskara.
Δ =(-7)² - 4.1.6
Δ =49 - 24
Δ =25
x= 7 ±√25 = x¹ = 7+5 = 12 = 6
2 x² = 7-5 = 2 = 1
Agora substitua o x por 6 e 1
√6+3 = 6-3 √1+3 = 1-3 {6}
√9 = 3 √ 4 = -2
3 = 3 CORRETO 2 = -2 FALSO
Antes de resolver uma equação assim temos que saber alguns assuntos que podemos chamar de pré-requisitos, e são eles: As quatro operações, potência, simplificação com radicais, operações com radicais, equações do primeiro e segundo graus e soma e produto dessas raízes, noções de função e zero da função. Depois de estudar esses assuntos fica muito fácil resolver uma equação irracional.
Equação irracional é aquela que no radical, nós encontramos uma incógnita, ou seja, uma letra.
Ex: √x = 15
Agora vamos ver como resolver uma equação irracional:
√x+3 = x-3
(√x+3)² =(x+3)² -->Iguala a potencia de acordo com o indice da raiz.
x+3 = x²-6x+9 -->Iguala a raiz a zero,reduzindo os termos.
x²-7x+6 = 0 -->Resolve fazendo a formula de Baskara.
Δ =(-7)² - 4.1.6
Δ =49 - 24
Δ =25
x= 7 ±√25 = x¹ = 7+5 = 12 = 6
2 x² = 7-5 = 2 = 1
Agora substitua o x por 6 e 1
√6+3 = 6-3 √1+3 = 1-3 {6}
√9 = 3 √ 4 = -2
3 = 3 CORRETO 2 = -2 FALSO
segunda-feira, 12 de julho de 2010
RESOLVENDO UMA EQUAÇÃO IRRACIONAL
Exemplo 1
1º passo: isolar o radical
2º passo: elevar os dois membros da equação ao quadrado
3º passo: organizar a equação
x2 - 10x +25 – x – 7 = 0
x2 - 11x + 18 = 0
4º passo: resolver a equação x2 - 11x + 18 = 0, aplicando o teorema de Bháskara.
∆ = (-11)2 - 4 * 1 * 18
∆ = 121 - 72
∆ = 49
x’ = (11+7)/2 = 9
x” = (11 – 7)/2 = 2
5º passo: substituir as raízes na equação original e verificar a igualdade.
x = 9
Portanto, 9 não serve.
x = 2
A única solução da equação é 2.
1º passo: isolar o radical
2º passo: elevar os dois membros da equação ao quadrado
3º passo: organizar a equação
x2 - 10x +25 – x – 7 = 0
x2 - 11x + 18 = 0
4º passo: resolver a equação x2 - 11x + 18 = 0, aplicando o teorema de Bháskara.
∆ = (-11)2 - 4 * 1 * 18
∆ = 121 - 72
∆ = 49
x’ = (11+7)/2 = 9
x” = (11 – 7)/2 = 2
5º passo: substituir as raízes na equação original e verificar a igualdade.
x = 9
Portanto, 9 não serve.
x = 2
A única solução da equação é 2.
SISTEMA DE EQUAÇÃO DO 2º GRAU COM DUAS INCÓGNITAS
A resolução de um sistema de duas equações com duas variáveis consiste em determinar um par ordenado que torne verdadeiras, ao mesmo tempo, essas equações.
ex: {x-y= 1 I
{x²+y²= 6 II
x= 1+y III
Utilizamos o método da substituição
=> Substituindo III em II
(1+y)²+y²=5
(1)²+2.(1).(y)+(y)²+y²=5
1+2y+y²+y²-5=0
2y²+2y-4=0
=> Formou-se uma equação do 2º grau. Então, resolvemos.
∆= (2)²-4.(2).(-4)
∆= 4+32
∆= 36
y= -2±√36 : 2.2
y¹= -2+6 : 4
y¹= 4:4
y¹= 1
y²= -2-6 :4
y²= -8 : 4
y²= -2
=> Substituimos y¹= 1 na incógnita I
x-(1)= 1
x-1= 1
x= 1+1
x= 2
=> Substituimos y²= -2 na incógnita I
x-(-2)= 1
x+2= 1
x= 1-2
x= -1
S= {2, 1; -1, -2}
(Enquanto x= 2, y= 1; enquanto x= -1, y= -2)
ex: {x-y= 1 I
{x²+y²= 6 II
x= 1+y III
Utilizamos o método da substituição
=> Substituindo III em II
(1+y)²+y²=5
(1)²+2.(1).(y)+(y)²+y²=5
1+2y+y²+y²-5=0
2y²+2y-4=0
=> Formou-se uma equação do 2º grau. Então, resolvemos.
∆= (2)²-4.(2).(-4)
∆= 4+32
∆= 36
y= -2±√36 : 2.2
y¹= -2+6 : 4
y¹= 4:4
y¹= 1
y²= -2-6 :4
y²= -8 : 4
y²= -2
=> Substituimos y¹= 1 na incógnita I
x-(1)= 1
x-1= 1
x= 1+1
x= 2
=> Substituimos y²= -2 na incógnita I
x-(-2)= 1
x+2= 1
x= 1-2
x= -1
S= {2, 1; -1, -2}
(Enquanto x= 2, y= 1; enquanto x= -1, y= -2)
EQUAÇÕES BIQUADRADAS
Toda equação tem uma forma geral que a representa, as equações biquadradas possuem a seguinte forma:
ax4 + bx2 + c = 0
Sendo que a, b e c podem assumir qualquer valor real desde que a seja diferente de zero. Veja alguns exemplos de equações biquadradas.
2x4 + 5x2 – 2 = 0; a = 2, b = 5, c = -2
-x4 – x = 0; a = -1, b = -1, c = 0
x4 = 0; a = 1, b = 0, c = 0
Observando as equações biquadradas percebemos uma de suas características: são equações onde os expoentes das suas incógnitas são sempre pares.
Para resolver esse tipo de equação é preciso substituir as incógnitas, tornando-a uma equação do segundo grau, veja os exemplos abaixo e compreenda como resolver passo a passo uma equação biquadrada.
Exemplo:
Resolva a equação biquadrada (x2 – 1) (x2 – 12) + 24 = 0. Devemos organizá-la primeiro, ou seja, tirar os parênteses e unir os termos semelhantes.
(x2 – 1) (x2 – 12) + 24 = 0
x4 – 12x2 – x2 + 12 + 24 = 0
x4 – 13x2 + 36 = 0
Agora devemos substituir a incógnita x2 por y.
x2 = y
x4 – 13x2 + 36 = 0
x2 . x2 – 13x2 + 36 = 0
y2 – 13y + 36 = 0
Resolvendo essa equação do segundo grau encontraremos como resultados de y’ e y’’ respectivamente os valores 9 e 4, como a incógnita da equação biquadrada é x, substituímos os valores de y na igualdade x2 = y e obteremos os respectivos valores de x.
Para y = 9
x2 = y
x2 = 9
x = ±√9
x = ± 3
Para y = 4
x2 = y
x2 = 4
x = ±√4
x = ±2
Portanto, a solução dessa equação biquadrada será {-3, -2, 2, 3}.
ax4 + bx2 + c = 0
Sendo que a, b e c podem assumir qualquer valor real desde que a seja diferente de zero. Veja alguns exemplos de equações biquadradas.
2x4 + 5x2 – 2 = 0; a = 2, b = 5, c = -2
-x4 – x = 0; a = -1, b = -1, c = 0
x4 = 0; a = 1, b = 0, c = 0
Observando as equações biquadradas percebemos uma de suas características: são equações onde os expoentes das suas incógnitas são sempre pares.
Para resolver esse tipo de equação é preciso substituir as incógnitas, tornando-a uma equação do segundo grau, veja os exemplos abaixo e compreenda como resolver passo a passo uma equação biquadrada.
Exemplo:
Resolva a equação biquadrada (x2 – 1) (x2 – 12) + 24 = 0. Devemos organizá-la primeiro, ou seja, tirar os parênteses e unir os termos semelhantes.
(x2 – 1) (x2 – 12) + 24 = 0
x4 – 12x2 – x2 + 12 + 24 = 0
x4 – 13x2 + 36 = 0
Agora devemos substituir a incógnita x2 por y.
x2 = y
x4 – 13x2 + 36 = 0
x2 . x2 – 13x2 + 36 = 0
y2 – 13y + 36 = 0
Resolvendo essa equação do segundo grau encontraremos como resultados de y’ e y’’ respectivamente os valores 9 e 4, como a incógnita da equação biquadrada é x, substituímos os valores de y na igualdade x2 = y e obteremos os respectivos valores de x.
Para y = 9
x2 = y
x2 = 9
x = ±√9
x = ± 3
Para y = 4
x2 = y
x2 = 4
x = ±√4
x = ±2
Portanto, a solução dessa equação biquadrada será {-3, -2, 2, 3}.
Assinar:
Comentários (Atom)